The Rossum Project / Papers / Calculations / Circle Path / Supplement	Revision 1.0 11 January 2006
Supplement To “A Path Following a Circular Arc” Using Calculus Methods

This webpage provides a supplement to the article A Path Following a Circular Arc to a Point at a Specified Range and Bearing. The original article used trigonometry methods to find functions for the position of a robot traveling along a path defined by the arc of a circle. Before its final derivation, however, the article mentioned that it was actually easier to find these results using calculus. In this supplement, we will show how to obtain the same results using calculus. Not only does the alternate approach involve fewer steps than the original, but it provides useful insights into the results.

Recall that in the main article we obtained with the following information:

Element	Description
	Specifiied initial position of robot.
	Specified initial orientation.
	Specified time of initial position.
	Specified fixed speed of travel.
	Derived rotational velocity (in radians/sec).
	Derived relationship giving orientation as a function of time.

We wish to find functions giving the x and y coordinates of the robot’s position as a function of time. These functions are not yet known, but from the information obtained so far we can construct their derivatives. Given the derivatives, we can use calculus methods to find the desired functions.

The functions x(t) and y(t) give the coordinates of the robot’s position. From calculus, we know that by taking their derivatives with respect to time – dx/dt and dy/dt – we have directional components of the robot’s motion. The derivative dx/dt gives us the change in the robot’s x coordinate with respect to time and the derivative dy/dt gives us the change in the robot’s y coordinate with respect to time. In other words, these derivatives give us the component of the robot’s velocity in the direction of the x-axis and the component of its velocity in the direction of the y axis.

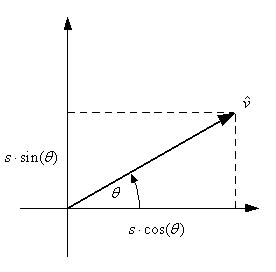
Figure 1 – Components of the velocity vector for the robot's motion.

Figure 1 shows how we find the velocity components for our robot’s motion. The velocity vector  is a combination of the robot’s speed and direction of travel. Its components give us the rates of change for the robot’s coordinates. And these rates of change are, of course, the derivatives that we need to find the robot’s position function.

From the relationships shown in the figure, and knowing the robot’s orientation as a function of time, we have

Integrating, we find

 and  are arbitrary integration constants. To find their values, we apply our knowledge about the initial conditions. We know that, at time , the robot is at position .

Substituting we have

and applying our initial condition gives us

We can apply a similar treatment for the y coordinate to obtain the robot’s position as a function of time

One final observation is worth noting.  The quotient  is just the turn radius  that was described in the main article. The sign of the value indicates the direction to which the robot is turning. If it is positive, then the robot is turning to the left. If it is negative, then the robot is turning to the right.