Except where otherwise noted, the following variables and coefficients are used in the calculations given below. While units don’t usually matter, angles are always measured in radius in a right-handed coordinate system (some results depend on this assumption).

Variable	Description
	Coordinates for position of robot.
	Orientation of the robot (in radians).
	Speed of the robot (always positive)
	Linear velocity of the robot (positive in forward direction)
a	Linear acceleration of the robot
	Rotational velocity of the robot
	Rotational acceleration of the robot
	Time variable.
	Set of parameters giving robot’s state – position, orientation, velocity, and rotational velocity – at time
	Velocity vector (combines speed and orientation).
	Robot’s position, x and y-coordinates as a function of time.
	Robot’s speed as a function of time.
	Robot’s acceleration as a function of time.
	Robot’s orientation as a function of time.
	Robot’s rotational velocity as a function of time.
L	Path length

Kinematics and Related Calculations

Straight-Line Trajectory

Reference: None

Description: Simple calculations for a trajectory following a straight line. Fixed velocity, zero rotational velocity.

Forward Calculations

Inverse Calculations

Given two points and

Length of path (distance between points or range from first point to last)

Bearing

The arc tangent, or inverse tangent, is sometimes written

In computational environments, the ATAN2 functions may be used.

Trajectory Following an Arc of a Circle

Description: Calculations with a fixed linear and rotational velocity.

Forward Calculations

Reference: Supplement to “A Path Following a Circular Arc” Using Calculus Methods

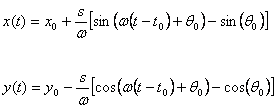
Note that the term is a signed quantity equivalent to the turn radius for the path.

Inverse Calculations

Reference: A Path Following an Arc of a Circle to a Specified Range and Bearing

Given a fixed speed and points and, find a circular path to target. Assume forward motion (see below).

Obtain range and bearing to goal position. Bearing should be in range (-180° to 180°).

Total rotation for trajectory

Turn radius (a signed quantity)

Linear distance of travel (length of circular arc)

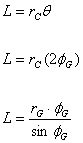
Compute delta time for travel

Compute rotational velocity

Find a function giving orientation as a function of time

Find a function giving position as a function of time

Special case: If the goal is behind the target then it may be more efficient for the robot to travel backward rather than forward. We do not change the value of the turn radius, but we do adjust to reflect the fact that the robot will be traveling a shorter distance in the opposite direction.

Trajectory Following a Cubic Polynomial

Description: A trajectory defined by a third-degree polynomial. Speed and acceleration are allowed to vary.

Reference: A Path Based on Third-Degree Polynomials, Constrained at its Endpoints by Position, Orientation, and Speed

Forward Calculations

Forward calculations are in the general form.

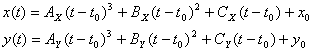
There are many ways to obtain third-degree polynomials for modeling a robot or vehicle trajectory. The following results assume that endpoint conditions are fully specified and so constitutes a forward kinematics treatment. Position, orientation, and speed values for times and are given. The derivation that follows produces a smooth path that resembles the classic cubic-spline method used for curve fitting (see picture below). Motion is always forward. See reference article for detailed explanation.

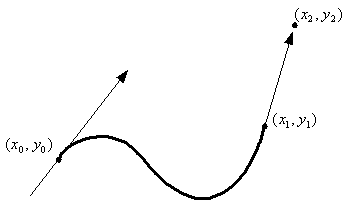Let

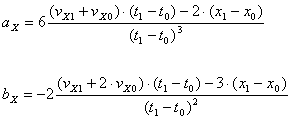
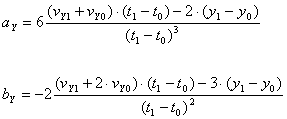
Then velocity and position calculations are given by

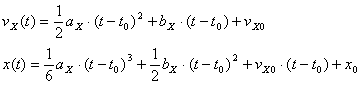
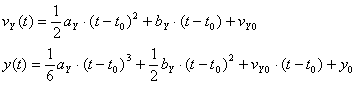
Inverse Calculations

The discussion on forward calculations above assumes that the duration time for the maneuver is known (and, thus, that the termination time is available). It is far more common that the duration time is unspecified and that the maneuver is constrained by performance issues related to the device (maximum speed or acceleration values). A duration time can be estimated using the results from the Trajectory following an arc of a circle notes above. Once an estimate is available, evaluate the resulting maximum speed and accelerations to see if they are within acceptable limits.

Taking and as the specified velocity vectors at the initial point and final point

Let

And

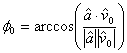
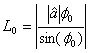
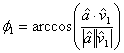
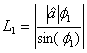
Use

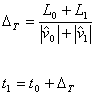
Recall that the term is equivalent to the specified speed at the corresponding point.

A Differentially Steered Drive System (with Odometry Calculations)

Description: A model for differential steering system (wheelchair-style steering and drive system).

Reference: A Tutorial and Elementary Trajectory Model for The Differential Steering System of Wheel-Based Actuators for Mobile Robots

Forward Calculations

Let

	be the rotational velocities of the left and right wheel, respectively
	be the radius of the wheels (assumed equal for both)
	be the distance between wheels (measured from tire center to tire center)

Assuming a constant rotational velocity for the wheels (and, thus, constant linear and rotational velocity for the robot)

Note that these equations follow the form described in Trajectory Following an Arc of a Circle above.

The term is a signed quantity equivalent to the turn radius for the robot.

Inverse Calculations (Odometry Calculations)

Given measurements from an encoder (odometer device), and assuming a constant rotational velocity for the wheels, we can estimate position and orientation using the following calculations

Let be the measured rotation of the left and right wheels, respectively.

Then

When the robot does not turn, but follows a straight-line path