|
The Rossum Project / Papers / Calculations / Glossary
|
Rev 1.0 16 January 2006 |
|
From “Calculations Useful for Robotics”
|
|
Introduction
This page gives brief explanations of terms that are used in Calculations Useful for Robots. This page is intended as a convenient reference, not the last word in robotics terminology. In virtually every case, you can find better references for these terms elsewhere on the web (I particularly encourage you to look at the Wikipedia). However, the explanations below focus on aspects of their subjects that feature most prominently in Calculations, and may serve to clarify issues from the articles.
As usual, I welcome all corrections and suggestions for improvements.
The Selected Terms
Ackerman Steering, Differential Steering, Omni-Directional Drive
Forward and Inverse Kinematics
Ackerman Steering, Differential Steering, Omni-Directional Drive
There are two, possibly three, systems generally used for locomotion in small, wheel-driven robots. Many small robots use a differential steering system (the system used in a wheelchair) or the Ackerman steering system (the system used in an automobile). In both these systems, it is impossible to completely decouple settings for orientation from position. For example, with an automobile type system, it is impossible to change the orientation of the robot without changing its position. And while it is possible for a robot with the wheelchair-like differential steering system to pivot in place, it cannot reach goal positions to its right or left without adjusting its orientation (for more information on differential steering systems, see A Tutorial and Elementary Trajectory Model for the Differential Steering System).
Some of the literature on the web refers to the Ackerman and differential steering systems as non-holonomic, meaning that you cannot specify one system parameter without affecting another. There is a third kind of wheel-driven actuator, the omni-directional drive, which is also used in small robots and happens to be truly holonomic. A robot or vehicle equipped with an omni-directional drive can move in any direction without changing its orientation and can change its orientation at any time without affecting its position or trajectory. There is something weird and almost ghost-like in the movement of an omni-directional drive, particularly as it moves across the floor in a straight line while rotating on its central axis. Building a robot that can do so is a pretty neat trick. Omni-robots require special compound wheels and the ability to coordinate at least three separate motors. Thus omni-directional robots are considerably less common than other drive systems.
Actuators and Wheels
An actuator is a device that allows a robot to interact with objects in its environment through the application of force. A gripper is a kind of actuator. It allows a robot to manipulate objects: pick them up, set them down, and crush them to bits when things go wrong. A motor-driven wheel is also a kind of actuator. It allows the robot to move by applying a force to the floor. A propeller is another kind of actuator. So is a fire extinguisher.
Actuators usually involve electro-mechanical devices like solenoids and motors. And, typically, the term “actuator” is used for macro-scale interactions. While a speaker fits the description of an actuator (an electro-mechanical device that imposes a force on the surrounding air), the movement it creates is on such a small physical scale that people generally do not think of it as an actuator.
Models and Calculations
A model is a representation of a system, device, or
phenomenon, that is usually expressed in the form of one or more equations. Typically,
a model captures the significant characteristics of a system, but may ignore
the secondary characteristics. For example, the equation 
is a model for the
behavior of an object falling freely near the Earth’s surface (
). As
models go, it is particularly simple. It neglects the potentially large effect
of air resistance. It neglects the rather lesser effect of the fact that the
acceleration due to gravity varies as a function of distance from the Earth’s center.
And it neglects the much smaller contributing factor that the Earth is not truly
spherical and that the force of gravity is different as you move farther from
the equator.
Of course, there’s no reason that we have to neglect all these contributing terms. And, in fact, if we were trying to accurately model the orbit of a satellite all of three would be important (even the effects of atmospheric drag). In general practice, though, simplified models are often more amenable than their elaborate counterparts. When we use the term “model” in Calculations Useful for Robotics, it almost always means that we are focusing on the major factors in the description of some phenomenon and are neglecting some low-order contributors.
For an accessible and well-written introduction to modeling and simulation, see http://www.systems-thinking.org/modsim/modsim.htm.
Functions and Mappings
A function is a mathematical object that accepts an input and returns an output. Although most of us think of a function in terms of equations, the actual definition in mathematics is far more general. I could not possibly do a better job of explaining the term “function” than the entry in the Wikipedia at http://en.wikipedia.org/wiki/Function_(mathematics)
Typically, we might write a function in the form
and say that “x is a function of t” where t is the input variable and x is the output. In Computations Useful for Robotics, we sometimes say that the function x(t) maps t onto x suggesting that the it projects values from one coordinate system to values in another. And we will sometimes describe a function as a mapping though this isn’t strictly speaking correct.
If you are unfamiliar with the concept of function, don’t be too quick to dismiss it as something mathematicians do just because they like very formal notation. It is a supple concept that proves itself worthy over and over again once you start applying math to practical purposes. And, if you still need convincing, read the article at the Wikipedia.
Kinematics and Dynamics
Kinematics and dynamics are both branches of mechanics. Kinematics focuses on motion but disregards the forces that cause that motion. Dynamics is concerned about the forces that cause motion. So kinematics is about effects, and dynamics is about cause and effect.
Forward and Inverse Kinematics
We use the term forward kinematics to describe problems where given certain facts about a robot’s motion – initial position, orientation, linear and rotational velocities, linear and rotational acceleration, etc. – we try to model its position as a function of time. In inverse kinematics we try to work the opposite problem. Given a desired target position and, perhaps, other constraints, we try to figure out what velocities and accelerations we need to apply to get the robot to its goal. Inverse kinematics often proves substantially more challenging problem than its counterpart. To get some sense of the relative effort involved, just think of how hard it is to invert a matrix as opposed to multiplying by one.
Encoders and Odometry
An encoder is a sensor that is coupled to a mechanical device to allow its position to be measured electronically. In mobile robotics, encoders are often mounted on the robot’s wheels, motors, or elsewhere in the drive chain to measure the rotation of the wheels. Essentially, these devices act as accurate odometers. The rotation of the wheels is used to estimate distance traveled. In turn, these estimates may be used to dead-reckon the robot’s position.
Encoders are subject to three kinds of error:
- Encoder resolution error (predictable)
- Mechanical error due to backlash in the gear chain, wheels out of alignment, or other factors (predictable)
- Interactions with its environment, loss of traction on slippery surfaces, etc. (unpredictable).
On a flat surface with good traction, odometry measurements can be quite accurate. Many implementations yield poor results because they do not account for issues such as acceleration (which complicates the arithmetic), or the predictable factors listed above. Still, even the best implementation will fail when it encounters unpredictable environment factors.
Backlash and Encoder Error
If you’ve ever adjusted the focus on a telescope, you’ve probably experienced backlash. When you turn the adjustment past the focus point, and then turn backward, there is a moment before the gears engage and the focus starts to change (I don’t own a very good telescope). This lag, which is called backlash, is due to small gaps between the teeth in the gears. As the gears turn in one direction, the teeth press together on one side. The gap in front of the teeth closes, and a gap opens behind. When the direction of the force-applying gear changes, it move to fill in the trailing gap and there is a brief period of rotation before the teeth mesh again.
If the encoder is mounted directly to the drive wheel, backlash does not factor into its measurements. But if there is some kind of gear train between the wheel and the encoder device, then backlash error may apply. Thus a wheel may turn several degrees without a change registering on the encoder.
So why not just mount the encoder directly on the wheel? Many implementations do, but wheel-mounted encoders often support only a very low resolution (measuring only a small number of encounter counts per revolution). In practice, the best way to avoid encoder error due to backlash is often a matter of avoiding the cause of backlash: changes in direction in the applied force on the gear chain.
Path and Trajectory
The terms path and trajectory are sometimes used interchangeably. The difference between the two is that path is pure geometry and trajectory is geometry combined with motion and time.
Dead Reckoning and Odometry
The English-language term “dead reckoning” probably doesn’t come from the phrase “deduced reckoning”, though that’s what many navigation books will tell you. It’s more likely that, in English, the term comes from the same source as the phrase “dead-on” meaning an accurate measurement. Or, perhaps, the word “dead” was chosen by a sailor with a dark sense of humor and a clear idea of what could happen if his navigation went wrong.
The term “dead reckoning” means navigation without a fixed external reference such as landmarks or stars that would allow a sailor to determine a ship’s position (while a compass does provide an external reference for orientation, it is not sufficient to determine position). The navigator estimates speed, direction, and time of travel starting from a known location and guesses where the ship (or robot) will end up after a specified period of time. In odometry, data about the robot’s position is derived from measurements made by encoder devices mounted to its wheels (i.e. data from odometers). By measuring the rotation and timing of the wheels, navigation software can estimate speed, turn rate, and distance covered. Thus odometry gives information about relative position. Combining that with information about the initial position and orientation, a robot can deduce its current position.
One of the problems with dead reckoning is that the effects of small errors in bearing estimates (orientation) tend to be magnified over time. Imagine, for example, that a navigator’s initial information about orientation is off by just 5 degrees. If the robot travels 10 meters (32.8 feet), its actual position will be 87,2 centimeters (34.3 inches) distant from its expected position.
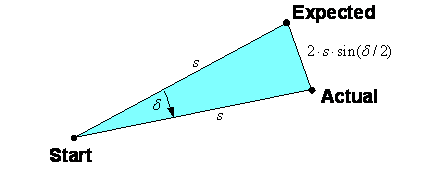
Figure 1 – Deviation over distance due to error (delta) in initial orientation data
Copyright © 2006 by G.W. Lucas. All rights reserved.